Actuellement, une grande partie des blockchains est basée sur le modèle de cryptage issu du hachage (arbre de Merkle), incorporé par Stuart Haber et W. Scott Stornetta à leur technologie d’horodatage (Haber& Stornetta, 1991), puis amélioré par Satoshi Nakamoto.
Pour ce qui est du fonctionnement de ces sécurisations, les deux principaux algorithmes utilisés pour le cryptage des transactions entre les différents acteurs sont l’algorithme symétrique et l’algorithme cryptographique asymétrique, qui utilisent tous deux le principe de hachage.
L’algorithme de hachage
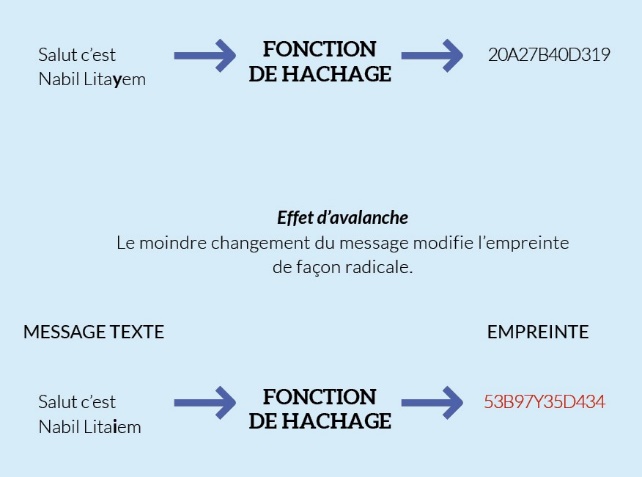
Le hachage est un principe complexe à la base de la sécurité de la blockchain. Dans cette technologie, il est le résultat d’une fonction mathématique, dite « de Hash », couplée à une hiérarchisation par arbre de Merkle. Pour simplifier, cette fonction prend des données et les convertit en une chaîne de chiffres et de lettres de taille/poids fixe presque unique de 256 bits (32 octets).
Figure 7. Fonctionnement d’un algorithme de hachage.
Adapté de Contributions méthodologiques à la conception et optimisation de systèmes embarqués, par N. Litayem, 2014, p. 145.
Illustration : Canva. Réalisation : les auteurs.
La cryptographie symétrique
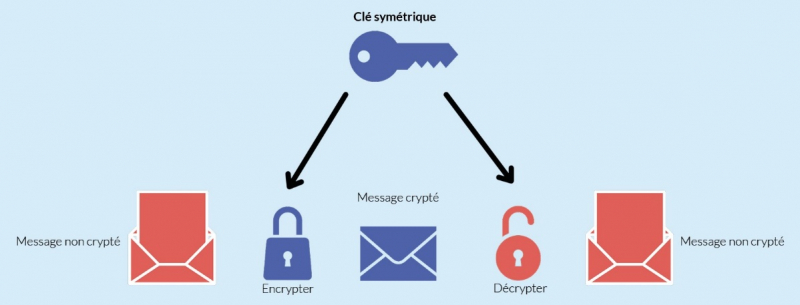
La cryptographie symétrique est la clef de chiffrement la plus ancienne. Elle est dite symétrique car elle fonctionne avec la même clef pour chiffrer et déchiffrer.
La cryptographie asymétrique
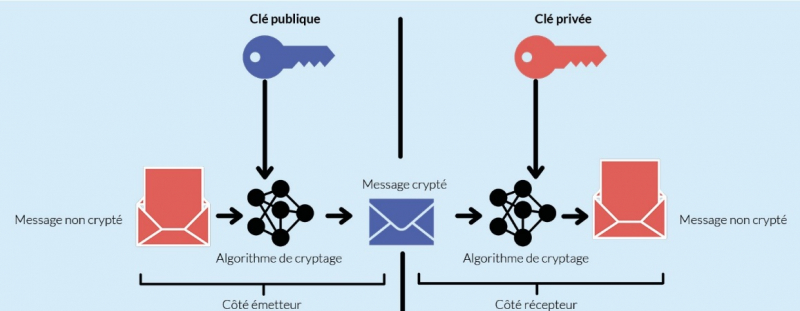
L’algorithme cryptographique asymétrique permet de crypter des informations et de les décrypter avec deux clefs différentes. Seules les deux personnes concernées par la transaction peuvent crypter/décrypter les informations.
Chaque tiers du réseau s’est vu attribué deux clefs :
-
une clef publique, pour la réception de la transaction au même titre qu’un IBAN, dans le milieu bancaire. Si vous donnez votre IBAN à une personne, théoriquement, elle ne pourra que vous transférer de l’argent ;
-
une clef privée, pour décrypter l’information reçue.
L’arbre de Merkle
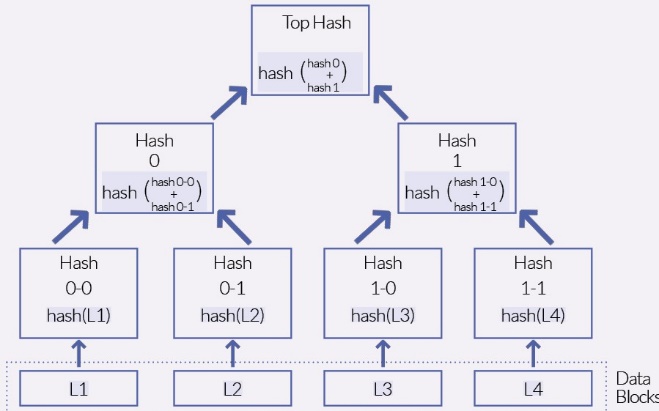
L’arbre de Merkle peut être vu comme étant composé de quatre feuilles (L1, L2, L3, L4) cryptées par hash cryptographique. Nous pouvons donc visualiser le hash de L1, L2, L3, L4. Cette méthode permet de compresser les informations par paire, donc hash L1 et hash L2 vont donner hash 0, le même mécanisme est appliqué pour le hash 1. Une dernière opération est nécessaire pour obtenir l’ultime niveau de l’arbre de Merkle, qui compresse le hash 0 et le hash 1 en un top hash. Cette « compilation » et ce « mélange d’informations » accroissent la sécurité au plus haut niveau.
Figure 8. Fonctionnement de l’arbre de Merkle.
Adapté de Software Heritage : pourquoi et comment construire la grande bibliothèque du code source, par R. Di Cosmo, 2017, Entreprises et histoire, 2.
Illustration : Canva. Réalisation : les auteurs.
Figure 9. Principe de fonctionnement d’un algorithme de cryptage symétrique.
Adapté de Contributions méthodologiques à la conception et optimisation de systèmes embarqués, par N. Litayem, 2014, p. 141.
Illustration : Canva. Réalisation : les auteurs.
Figure 10. Principe de fonctionnement d’un algorithme de cryptage asymétrique.
Adapté de Contributions méthodologiques à la conception et optimisation de systèmes embarqués, par N. Litayem, 2014, p. 14.
Illustration : Canva. Réalisation : les auteurs.
Configuration d’une chaîne de blocs : l’exemple du bitcoin
Pour illustrer l’organisation d’une chaîne de blocs, prenons pour exemple celle du bitcoin. Bien que toutes les blockchains ne soient pas composées de cette façon, celle-ci est plus accessible et permet une meilleure visualisation.
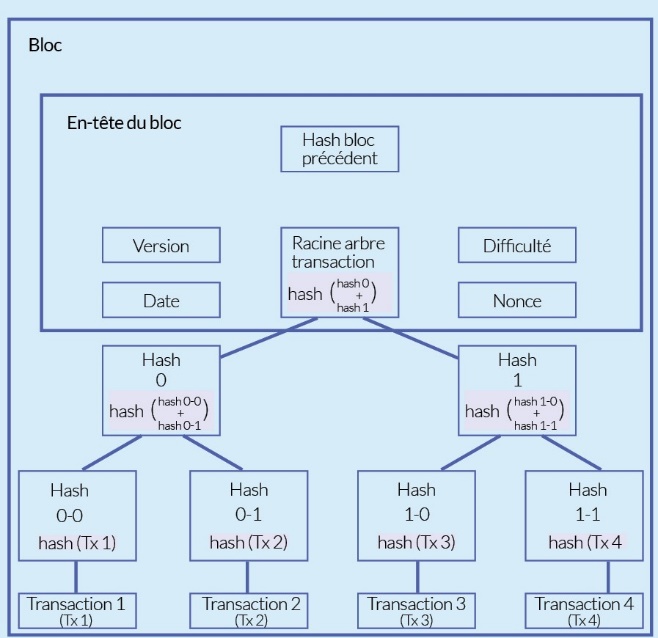
La blockchain est constituée de plusieurs blocs en série les uns à la suite des autres. L’intérieur d’un bloc du réseau bitcoin est composé :
-
d’un « en-tête », avec le numéro de la version, l’identification du précédent bloc et les informations de cryptage par hachage. Cet « en-tête » contient aussi l’horodatage et le nonce, qui est un morceau de programme permettant d’ajouter des 0 dans le hash afin de remplir les petits blocs, insérés eux-mêmes dans le grand bloc ;
-
de blocs « transaction », qui renferment les informations de l’acquéreur et du vendeur. Nous pouvons observer le montant de la transaction et les clefs publiques de destination de la transaction.
Le hash du bloc antérieur est composé des informations permettant d’identifier le bloc précédent, ainsi que le hash des transactions actuelles ; c’est un peu comme l’identification du bloc.
Dans la méthode d’inscription des informations dans une chaîne de blocs, il faut donc passer par plusieurs étapes, surtout dans la blockchain du bitcoin : le cryptage et le décryptage, la vérification des informations et la validation des blocs. Le bitcoin fonctionne suivant un consensus reposant sur la preuve de travail, le minage (Marin-Dagannaud, 2017, p. 43).
Figure 11. Organisation d’un bloc du bitcoin.
Adapté de Comprendre la blockchain Ethereum – Article 1 : Bitcoin, première implémentation de la blockchain (2/2), par G. Marin-Dagannaud, 2016.
Illustration : Canva. Réalisation : les auteurs.